Converting an NFA to DFA
Procedure for converting a non-deterministic finite automata to a deterministic finite automata.
Part of my notes from ITEC 420 "Computability Theory and Formal Languages" at Radford University, Fall 2015
Given an NFA
Like this one, for instance:
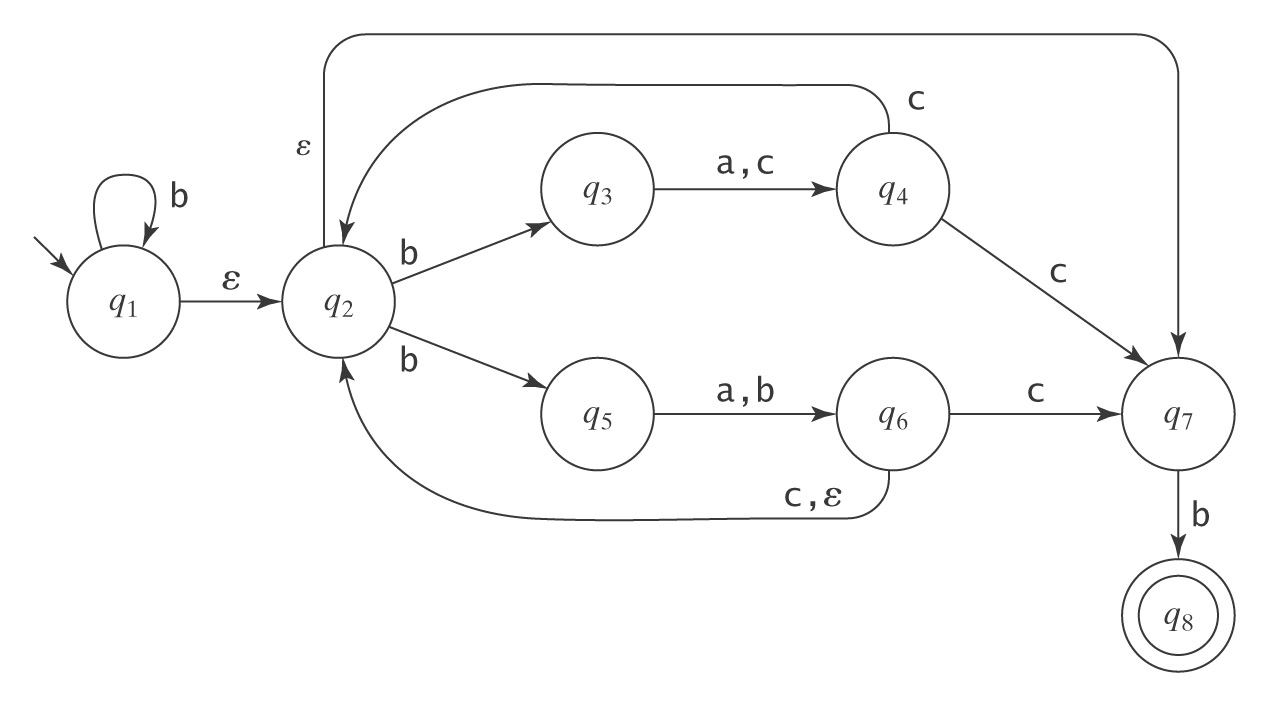
We can represent that machine as a table like this:
q |
eps(q) |
a | b | c |
|---|---|---|---|---|
| 1 | {1,2,7} | - | 1 | - |
| 2 | {2,7} | - | 3,5 | - |
| 3 | {3} | 4 | - | 4 |
| 4 | {4} | - | - | 2,7 |
| 5 | {5} | 6 | 6 | - |
| 6 | {2,6,7} | - | - | 2,7 |
| 7 | {7} | - | 8 | - |
| 8 | {8} | - | - | - |
- The
qcolumn is all the states in the NFA (for simplicity, we're
writing qN as just N) - The columns
a,b, andcshow the states reachable froms
for a particular input symbol. eps(q)is the set of all states reachable from that state without
consuming any input.- We don't need the eps column to represent the table, it will just be helpful later
Building the DFA
The states in our DFA will each be a set of states from the NFA.
A helpful function overload:
eps : states -> set of states
eps : set of states -> set of states
We'll define the eps of a set of states as the union of the eps of each of the states in the input, roughly like so:
func eps(states: Set<State>) -> Set<State> {
if not states.isEmpty {
return eps(states.first).union(eps(states.rest))
} else {
return Set<State>()
}
}
We want to end up with a table showing all the states in the DFA and all their transitions. How do we do that?
First, the new starting state s' is eps(s) = {1,2,7}.
Then, figure out all the states that can be reached from all the states in that set
for each of the symbols in the alphabet.
For instance, by checking our first table from above, we see that for states 1, 2, and 7
an input of a goes nowhere. We'll represent that in our DFA with the empty set {}.
For an input of b, from 1, 2, or 7 we could reach 1, 3, 5, or 8. However, we have to
account for the possibility of epsilon transitions, which we can't represent directly
in the DFA. In the DFA, the set of states reachable from {1,2,7} on b will actually
be the eps of the states directly reachable... so our result will be eps({1,3,5,8}).
This is where the extra eps(q) column in our table comes in handy. eps({1,3,5,8}) =
eps(1) union eps(3) union eps(5) union eps(8), or {1,2,3,5,7,8}.
We've just found another state in our DFA. We know that the starting state is {1,2,7},
and on an input of b it will transition to the state {1,2,3,5,7,8}.
The first rows in the table for our new DFA will look like this:
| q' | a | b | c |
|---|---|---|---|
| {1,2,7} | {} | {1,2,3,5,7,8} | {} |
| {1,2,3,5,7,8} | ... | ... | ... |
Since we've found a new state, we need to figure out the transitions from that state as
well. It might yield more new states, which will get their own rows in the table, and
so on, until we've found all the transitions. At some point, the results of all the
transitions will be states that we've already seen at least once, so no new rows will be added to the table.
Here's the final table:
| q' | a | b | c |
|---|---|---|---|
| {1,2,7} | {} | eps({1,3,5,8}) = {1,2,3,5,7,8} | {} |
| {1,2,3,5,7,8} | eps({4,6}) = {2,4,6,7} | eps({1,3,5,6,8}) = {1,2,3,5,6,7,8} | eps({4}) = {4} |
| {2,4,6,7} | {} | eps({3,5}) = {3,5,8} | eps({2,7}) = {2,7} |
| {1,2,3,5,6,7,8} | eps({4,6}) = {2,4,6,7} | eps({1,3,5,6,8}) = {1,2,3,5,6,7,8} | eps({2,4,7}) = {2,4,7} |
| {4} | {} | {} | eps({2,7}) = {2,7} |
| {3,5,8} | eps({4,6}) = {4,6} | eps({6}) = {2,6,7} | eps({4}) = {4} |
| {2,7} | {} | eps({3,5,8}) = {3,5,8} | {} |
| {4,6} | {} | {} | eps({2,7}) = {2,7} |
| { 2,4,7} | {} | eps({3,5,8}) = {3,5,8} | eps({2,7}) = {2,7} |
| {2,6,7} | {} | eps({3,5,8}) = {3,5,8} | eps({2,7}) = {2,7} |
Accept states:
In the original machine, the accept state was q8. In order to accept the same inputs,
the DFA accept states will be any state containing q8.
\(A' = {q' \in K' : \exists q \in q' : q \in A}\)
The machine represented by this table, when drawn out, looks something like this:
