Creating an Equivalent Regular Expression for a Finite State Machine;
Part of my notes from ITEC 420 "Computability Theory and Formal Languages" at Radford University, Fall 2015

Given:

Language:
\[L=\{w \in \{a,b\}^* : \text{every } a \text{ is immediately followed by a } b \}\]

Machine:

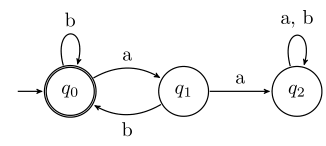
Preparation

For many smaller machines, you can get by on intuition and not do this. But this is required for the procedural, algorithmic solution to work.

1. Add additional start and end states

Replace the existing start state by adding a new start state with a single transition on epsilon to the original start state. (We will arbitrarily name this state q_s, for "start".)

Create a new accept with epsilon transitions from all the original accept states to this new state. Change the original accept states to non-accept states. (We will arbitrarily name this state q_e, for "end".)

The important property for these two new states is that the new start state will only have transitions out, and the new end state will only have transitions in.

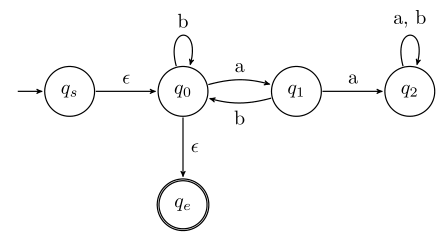
2. Replace transitions on multiple symbols with a union

If there is more than one transition between two states, or a transition on more than one symbol (which is effectively the same thing), these should be replaced with a union RE.

For instance, in our example machine, there are two transitions ((q₂, a), q₂) and ((q₂, b), q₂), represented by a single loopback arrow on state q₂. This transition should be re-labelled with the regular expression \(a \cup b\).

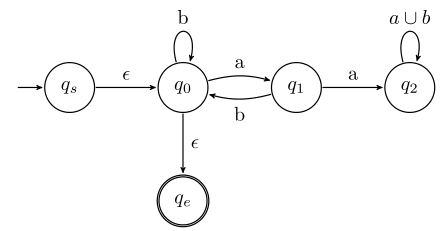
3. Add null transitions

Every state must be connected to every other state. Every state in the original machine must have a transition to every other state in the original machine, including itself. If one does not exist already, add a null transition (a transition on the empty RE \(\varnothing\)). Also add null transitions from the new start state added in 1 to every other state (except to the original start state, which already has an epsilon transition). Add a null transition from all the original non-accept states to the new end state (the original accept states should already have epsilon transitions to the new end state from 1).

At the end, every state will be connected somehow to every other state, except that the start state will still only have outbound transitions and the end state will still only have inbound transitions (so these two will not have loopback transitions to themselves.)

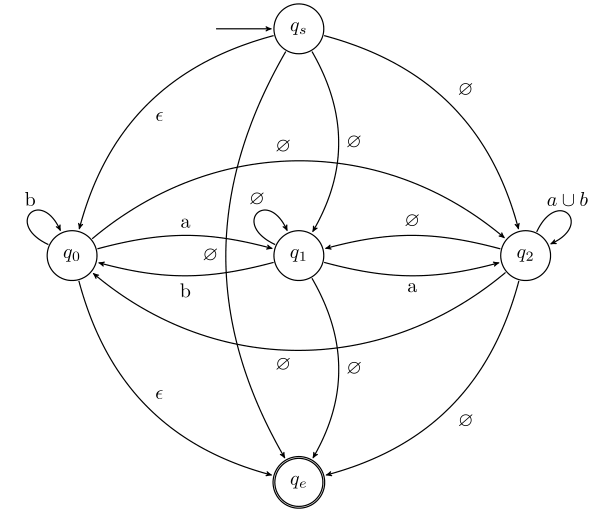
4. Table representation

With all those null transitions, the diagram is a little nuts - and it gets even more nutes the more states there are in the machine. It may be helpful to represent the modified machine as a transition table:

The rows are the origin states for the transitions (note the empty row for q_e), and the columns are the destination states for the transitions (note the empty column for q_s). So for example, the transition from q₀ to q_e is \(\epsilon\), and the transition from q₂ to q₂ (a loopback) is a, b.

Removing states

To generate the regular expression, we repeatedly remove original states from the machine, until only the new start and end states remain. At each step, we replace the transitions involving the state we removed with equivalent transitions labelled using a regular expression rather than a set of symbols from the machine's alphabet. At the end, there will only be two states (q_s and q_e) and one transition, labelled with a regular expression which is equivalent to the original machine.

1. Remove a state

Pick one of the original states to remove. When running on intuition, pick states that are more isolated. But when following the procedural solution exhaustively, it doesn't matter which one you pick. Call it rip (we're ripping it out). We'll start by removing state q₂.

2. Create pairs of remaining states

Determine all possible transitions in the new machine. The most straightforward way to do this is to construct a new table without the state we want to remove. For instance:

There won't be any transitions into S, or out of E, so we need to figure out the transitions shown with a ?.

3. Determine new transitions

The formula to create a regular expression for one of these transitions is:

\(RE_{transition} = R(p, q) \cup R(p, rip) R(rip, rip)^* R(rip, q)\)

Where \(R(s_1, s_2)\) returns the existing pattern for a transition from s₁ to s₂.

If we pick an origin state p and a destination state q, then the new transition from p to q will be the direct transition from p to q unioned with the concatenation of the transition from p to the state being removed, the transition from the state being removed to itself, and the transition from the state being removed to q. (This is why we had to add all those null transitions - this formula would not work uniformly unless each of these transitions exists!)

For example, the new transition from q₀ to q₁ would be:

\[ rip = q_2 , p = q_0 , q = q_1 \\ \\ R(q_0, q_1) = a \\ R(q_0, q_2) = \varnothing \\ R(q_2, q_2) = a \cup b \\ R(q_2, q_1) = \varnothing \\ \\ t = R(q_0, q_1) \cup R(q_0, q_2) R(q_2, q_2)^* R(q_2, q_1) \\ = a \cup \varnothing (a \cup b)^* \varnothing \\ = a \cup \varnothing \\ = a \]

This is consistent because before removing the state, there was not path from q₀ to q₁ that passed through q₂. Therefore, after removing q₂ the transition from q₀ to q₁ remains unchanged.

Here are the rest of the transitions after removing q₂:

• \((q_s, q_0) = R(q_s,q_0) \cup R(q_s,q_2) R(q_2,q_2)^* R(q_2,q_0) = \epsilon \cup \varnothing (a \cup b)^* \varnothing = \epsilon \cup \varnothing = \epsilon\)
• \((q_s, q_1) = R(q_s,q_1) \cup R(q_s,q_2) R(q_2,q_2)^* R(q_2,q_1) = \varnothing \cup \varnothing (a \cup b)^* \varnothing = \varnothing\)
• \((q_s, q_e) = R(q_s,q_e) \cup R(q_s,q_2) R(q_2,q_2)^* R(q_2,q_e) = \varnothing \cup \varnothing (a \cup b)^* \varnothing = \varnothing\)
• \((q_0, q_0) = R(q_0,q_0) \cup R(q_0,q_2) R(q_2,q_2)^* R(q_2,q_0) = b \cup \varnothing (a \cup b)^* \varnothing = b \cup \varnothing = b\)
• \((q_0, q_e) = R(q_0,q_e) \cup R(q_0,q_2) R(q_2,q_2)^* R(q_2,q_e) = \epsilon \cup \varnothing (a \cup b)* \varnothing = \epsilon \cup \varnothing = \epsilon\)
• \((q_1, q_0) = R(q_1,q_0) \cup R(q_1,q_2) R(q_2,q_2)^* R(q_2,q_0) = b \cup a (a \cup b)^* \varnothing = b \cup \varnothing = b\)
• \((q_1, q_1) = R(q_1,q_1) \cup R(q_1,q_2) R(q_2,q_2)^* R(q_2,q_1) = \varnothing \cup a (a \cup b)* \varnothing = \varnothing\)
• \((q_1, q_e) = R(q_1,q_e) \cup R(q_1,q_2) R(q_2,q_2)^* R(q_2,q_e) = \varnothing \cup a (a \cup b)* \varnothing = \varnothing\)

The filled in table is:

A diagram of the machine after removing q₂ is:

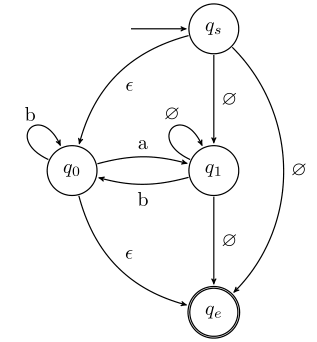
In this case, it would be fairly straightforward to determine the new machine without explicitly working out all 9 of the transitions - they "new" transitions are the same as they were before! The real utility of using this procedure is in later steps or more complicated machines.

4. Repeat

Continue removing states, combining transitions into regular expressions, until only q_s and q_e remain. The regular expression labelling the transition from q_s to q_e should be equivalent to the original finite state machine (that is, it generates the same set of strings that the machine accepts).

Solution

Remove State 1

• \((q_s, q_0) = \epsilon \cup \varnothing \varnothing^* b = \epsilon\)
• \((q_s, q_e) = \varnothing \cup \varnothing \varnothing^* \varnothing = \varnothing\)
• \((q_0, q_0) = b \cup a \varnothing^* b = b \cup a \epsilon b = b \cup ab\)
• \((q_0, q_e) = \epsilon \cup \varnothing \varnothing^* \varnothing = \epsilon\)

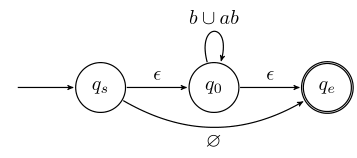
Remove State 0

• \((q_s, q_e) = \varnothing \cup \epsilon (b \cup ab)^* \epsilon = (b \cup ab)^*\)

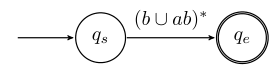
So, the original machine is equivalent to the regular expression \((b \cup ab)^*\).